ПОКАЗАТЕЛИ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМОГО ЭЛЕМЕНТА

Для того чтобы найти показатели, харак­теризующие надежность восстанавливаемого элемента, необходимо определить какую-либо модель его функционирования. Простейшей является такая модель, при которой элемент какое-то случайное вре­мя ті работает до первого отказа, фиксируемого достоверно, затем следует мгновенное и полное восстановление свойств элемента в мо­мент U = Ті, после чего элемент снова работает случайное время т2 до второго отказа, определяемого достоверно, затем мгновенно восста­навливается до начального состояния в момент t2 = Ті + т2 и т. д. Для определенности полагают, что в начальный момент времени элемент работоспособен (рис. 2.12).

Моменты отказов tlt t2, …, tt, …, tm образуют случайный поток, или процесс, отказов, а так как восстановление следует мгновенно, то — mi же моменты образуют случайный поток, или процесс, восстанов­ления. Процесс восстановления можно описать случайной величиной r(t), равной числу отказов, происшедших за время t. Естественно, что r(t) принимает только целые неот­рицательные значения.

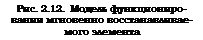Величину r(t) можно характе­ризовать математическим ожида­нием числа отказов, происшедших на интервале (0, t),

Mlr{t) = Q(0, (2.101)

которое обычно называют ведущей функцией потока (см. 124]) или функцией восстановления (см. 119, 20, 361). Часто удобно использо­вать функцию

Ш(0=^, (2.102)

at

которую называют плотностью восстановления.

Функцию «(/) можно интерпретировать как среднее число kco(i)At восстановлений в интервале времени (/, t + ДО. если одновременно — идет очень большое число k независимых процессов.

Случайная величина r{t) имеет распределение с законом

вер[г(0 ;> т = Plr(t) > т] = P(ti + т2 + … + тг + … +

+ тт< 0 = (2.103)’

т

где Fm(t) — закон распределения случайной величины trn — И тг.

i—I

Вероятность того, что за время t не будет ни одного восстановления (отказа),

Plr(t) = 01 = P0(f) = 1 — />(п < 0 = 1 — Щ, (2.104)

где F(t) = Ft(t) — обозначение, которое будет использовано далее.

В общем случае вероятность того, что за время t будет ровно т восстановлений (отказов), определяется зависимостью

Plr(t) = т] = Pm(t) = Fm{t) — Fm+i(t). (2.105)

По определению математического ожидания и с учетом (2.105) имеем

а Ю = М г (Щ = 2 tnPm (/) = 2 tn[Fm (t) — Fm+l (/)] =

m=1 m—

2 — 2 fflfm+i(0= 2 rnFm(f)-

m=I m=I m=I

— (m-l)Fm(0= 2 ^m(0-

m=2 1

Соответственно

оо оо

= = ип (2107)

т~ I т=1

где /т(/) — плотность вероятности случайной величины tm.

Математическое ожидание числа отказов на произвольном интер­вале (/i, t2)

Q(tu t2) = Q(t2) — ОД, (2.108)

или

f2

Q(ti, ti)= (o(t)dt. (2.109)

І

Можно показать (см. (361), что функция £2(/) всегда конечна и удов­летворяет интегральному уравнению

t

Q.(t) = F{t)+^D.(t~r)dF(x). (2.110)

о

Дисперсия числа восстановлений или отказов r(t) по определению и с учетом (2.110) определяется зависимостью (см. Г19])

t

D[r(0] = 2 (■&(? — т)<Ш(т)+£!(/) — а2(/) (2.111)

6

Функция Fm(t) является m-кратной сверткой функции F(f), и ее определение в общем случае достаточно сложно. При некоторых ви­дах закона распределения F(t) можно получить удобные формулы для введенных выше показателей надежности восстанавливаемого элемен­та, если восстановление происходит мгновенно.

Для случая экспоненциального закона распределения времени между восстановлениями или отказами, когда в соответствии с (2.104)

Fi (t) = F(t) = 1 — е-и и Р0= 1 — F(t) = e~u,

процесс восстановления является пуассоновским потоком и в соот­ветствии с (2.1) вероятность получения ровно т восстановлений (от­казов)

Р [Г (t) = m3 — Рт (0 = е-м, (2.112)

где },t —- математическое ожидание числа восстановлений (отказов) на интервале (0, t).

Действительно, математическое ожидание числа восстановлений на интервале (0, t) по определению с учетом (2.112) принимает вид

т = Я і,

т. е.

(2.113) (2.114)

п(0 — ял

Тогда

сШ (t) dt

к>(/) = Я.

 

Вероятность получить за время / не более /п отказов в соответствии г (2.112) может быть вычислена как сумма получения і = 0, 1, 2, …, т отказов:

рио < т] = 2 Ph{t) = S е~м ’ (2Л!5>

6=0 /г—0 *’

Если вероятность P[r(t) < т]=» а задана, то параметр закона Пуас­сона а = Я/ является квантилью распределения Пуассона:

(2.116)

Используя табл. П.7 квантилей Пуассона при а = 1 — уь по

заданным значениям а„ и а можно найти т = т или по известным аа и ш определить величину а.

Таким образом, для экспоненциального закона плотность восста­новления, или параметр потока отказов (см. [24]), т. е. среднее число отказов восстанавливаемого элемента в единицу времени, численно равно интенсивности отказов Я невосстанавливаемого, работающего до первого отказа элемента, хотя величина Я является условной плот­ностью вероятности того, что невосстанавливаемый элемент, про­работавший до времени t безотказно, откажет на интервале (/, t + А/), а со(0 — безусловная плотность вероятности отказа (восстановления) восстанавливаемого элемента в момент t.

Если интервалыт,, тг,…, тг, … (рис. 2.12) между соседними восста­новлениями (отказами) распределены нормально, то случайная ве­личина tm = t = т, + т2+— + тг + + тт как линейная функция

от независимых нормально распределенных величин имеет также нор­мальный закон с математическим ожиданием

МШ = тТ0, (2.117)

іде Т„ — среднее время безотказной работы элемента.

оо

В соответствии с (2.11)Т0= [ P(t)dt. Для случая, когда в нормаль-

о

ном распределении Т0 > о, где а — среднее квадратическое отклоне­ние интервала между отказами, функция P(t) может быть представ­лена в виде (см. [19])

-*•/2 і e dx= 1

где Ф„ (x) — табличная функция (см. табл. П. З).

Дисперсия случайной величины t — tm может быть найдена в виде

где D[t] = о2 — дисперсия времени между соседними отказами.

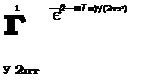В соответствии с (2.117) и (2.118) закон распределения случайной величины t принимает вид

а математическое ожидание числа отказов или восстановлении за время t в соответствии с (2.106) определяется выражением

т=1 m=1 ‘

… VI І — Ц-тТ^/Рт*) Ю (0 = > ,——— т=г е = ZjI

где Ф0(х) — табличная функция (см. табл. П. З).
Соответственно плотность восстановления

где /(x) — табличная функция (см. табл. П.2).

Часто бывает важным установить асимптотические свойства про­цесса восстановления, т. е. его характеристики при большом времени /, после того как наблюдалось большое количество отказов при про­извольном законе F(t). При изложении этого вопроса воспользуемся результатами, полученными в работе 1191. Можно показать, что

(2.122)

i-+oo t Т о

т. е. для длительного участка времени t среднее число отказов, прихо­дящихся на единицу времени, является величиной, обратной средне­му времени жизни элемента, а математическое ожидание числа отка­зов для большого t можно находить по приближенной зависимости

M[r(t) = Q(/) « /УГ0 + ст2/(2Г0) — 1/2, (2.123)

где о2 — конечная дисперсия времени между отказами.

При этом случайная величина r(t) имеет асимптотически нормальное

Полученные выше зависимости справедливы для простейшего про — • цесса восстановления (мгновенное и полное восстановление свойств элемента при достоверно фиксируемом отказе). На практике время вос — [1] [2]

законом G(t) = Р(тв< /), характеризуемым математическим ожида­нием Mlтв] — Т2 и средним квадратическим отклонением а2 = Д £>[ть1.

Важнейший показатель надежности такого элемента — коэффи­циент готовности Kr(t), представляющий собой вероятность того, что элемент окажется работоспособным в произвольный момент вре­мени t.

Функция Kr(t) ДЛЯ произвольного момента времени может быть найдена по зависимости (см. [19])

t

KT(t)= 1—/40+ pi—F(f —*)]0>а(х)Лс, (2.127)

о

где (о2(х) — плотность восстановления, характеризующая поток (2.126).

В практических задачах обычно используют стационарное значе­ние коэффициента готовности /Сг, к которому стремится функция Кг(0 при /->-оо. Можно показать, что

Kr = lim КТ (/) = Т11(Т1 + Т2),] (2.128)

t-+co

т. е. стационарное значение коэффициента готовности есть математи­ческое ожидание времени, в течение которого элемент находится в ра­ботоспособном состоянии. Обычно это значение и называют коэффи­циентом готовности элемента. Доказано [19], что случайные величины числа отказов r(t) и числа восстановлений rB(t) за время /, отличающие­ся друг от друга не более чем на единицу, распределены асимптоти­чески нормально с математическим ожиданием и дисперсией

tl(Tt + т2) и (о? + о!)//(Г, + Т2)3. (2.129)

Результат (2.129) совпадает с (2.124) для потока с мгновенным вос­становлением при То — Ті г Т2 или Та — Ти Тг = 0; о2 = о? + а!’, о2 = о?; а! = 0. Если длительность безотказной работы и длитель­ность восстановления распределены по экспоненциальным законам F(t) — 1 — е~и и G(/) = 1 — е _|L/, где р — плотность восстанов­ления или параметр потока восстановления, то коэффициент готовности

элемента (ель [19])

Кг (/) = (ц + ЯеГ(Х+|1) ‘)/(р + Я). (2.130)

Стационарное значение этой величи­ны

Kr = lim Кг (0 = ц/(ц + Я). (2.131)

со

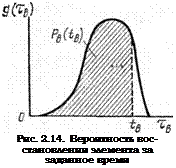
Важным показателем надежности восстанавливаемого элемента является также вероятность восстановленияР B(t в) за заданное время /в, т — е — вероятность того, что случайная величина тв с плотностью вероятности g(iB) меньше

заданного значения tB (рис. 2.14):

Если время восстановления имеет экспоненциальное распределе­ние с плотностью вероятности

g(TB) = pe—^в, (2.133)

то в соответствии с (2.132) и (2.133) получим

_ _____________ .

р* (*,) = j! ie ^dxa = 1 — е * в. (2.134)

о

В соответствии с определением математического ожидания среднее время восстановления

і) дисперсия

Таким образом, для экспоненциального распределения времени восстановления Ті — 1/р, а дисперсия of = 1/р2.

Для случая, когда тв имеет нормальное распределение с плотно­стью

і — (vr* )2/(2а*)

, У~2л

за время tB вероятность восстановления

где Ф0(х) — табличная функция (см. табл. П. З).

Характеристикой надежности восстанавливаемого элемента явля­ется также суммарная наработка S за время t, включающая в себя сумму всех периодов работы элемента ть причем последний период может быть неполным. В работе [19] показано, что случайная величи­на S асимптотически нормально распределена с математическим ожиданием и дисперсией соответственно

77/(7, + Т2) и ТТ (о?/Т? + сУт1)Ц(7 + 7а)3. (2.136)

Проиллюстрируем возможности использования полученных выше формул для расчета показателей надежности восстанавливаемых элементов.

Пример 2.8. Найти математическое ожидание О (/) числа отказов за три года для мгновенно восстанавливаемого элемента, если время между соседними отказами имеет. экспоненциальное распределение с параметром X = КГ4ч~4.

В соответствии с (2.113) и с учетом того, что три года составляют t = = 3 • ЗС5 — 24 = 26280 ч, имеем Q(f) = КГ4 • 26280 = 2,628.

Пример 2.9. В условиях примера 2.8 найти такое значение параметра X, при котором за три года число отказов т элемента с вероятностью а = 0,90 бу­дет не более пяти.

По табл. П.7 для а = 0,90 и т = 5 находим аа = Xt = 3,152, откуда X = 3,152/< = 3,152/26280 = 1,199 • Ю’4 ч-1.

Пример 2.10. В условиях примера 2.8 найти вероятность того, что за три года элемент откажет ие более пяти раз.

Параметр распределения Пуассона а = Xt = 10-4 • 26280 = 2,628.

По табл. П.7 при аа = 2,628 и т = 5 найдем а « 0,949.

Пример 2.11. Для элемента с мгновенным восстановлением найти закон распределения числа отказов за 10 лет эксплуатации, если среднее время жизни элемента (математическое ожидание работы между двумя смежными отказами) Т0 = 1000 ч, а среднее квадратическое отклонение (Т = 100 ч.

Учитывая, что t — 10 лет = 10 • 365 • 24 = 87 600 ч достаточно велико по сравнению с Т0, можно использовать асимптотически нормальное распределение. Параметры этого распределения могут быть найдены в соответствии с (2.124): математическое ожидание числа отказов tlT0 = 10 * 365- 24/1000—87,6; дис­персия o*tlT03 = 1002 • 87600/1000s = 0,876.

Плотность вероятности случайной величины r(t) числа отказов за время t принимает вид

1 — (г—87,6)«/(2-0,876)

f (г) = ————- —г е

0,876 УШГ

Пример 2.12. В условиях примера 2.11 найти вероятность того, что число отказов элемента за 10 лет не превысит 90.

Искомая вероятность определяется табличной функцией (см. табл. П.3)

90

Р (г < 90) = (г) dr = Фо[(90 — 87,б)/|АоТ87(Г|= Ф0 (2,564) =

о

= 0,994826 0,995.

Пример 2.13. Рассчитать коэффициент готовности к пятому году работы для элемента с конечным временем восстановления, если среднее время жизни элемента Ті = 5000 ч, а среднее время восстановления Т2 = 500 ч. Так как эле­мент проработал 5 • 8760 = 4380 ч, то по зависимости (2.128) найдем установив­шееся значение коэффициента готовности:

кг = Тії (Ті + Т2) = 5000/(5000 + 500) « 0,9091.

Используя (2.130), найдем изменение функции:

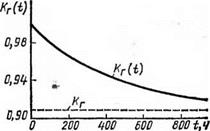
Кт (<) = (0,002 + 0,0002е— <0’0002+0,0°2) 0/(0,002 + 0,0002) —

= 0,9091 + 0,09091е~0,(ю22/.

О 100 200 300 500 1000 2000 3000

1<г(1)…, 1,0000 0,9821 0,9070 0,9561 0,9394 0,9192 0,9102 0,9092

Таким образом, за время /, меньшее математического ожидания времени жизни элемента Тг = 1 /Я = 5000 ч, т. е. в среднем еще до первого отказа элемен­та, функция Kr(t) сходится к стационарному значению.

Пример 2.15. Рассчитать вероятность Рв(/„) восстановления элемента за время tB — 100 ч, если случайное время восстановления распределено экспоненциально с параметром р = 0,02 ч-1.

В соответствии с (2.134)

, (/„) = I — е = 1 — е =0,8647.

Пример 2.16. В условиях примера 2.15 Найти время, за которое элемент будет восстановлен с вероятностью 0,99. На основании (2.134) имеем

/в = —Jn[ 1 — Рь(/в)]/ц =

=—1п(1 — 0,99)/0,02 я» 230,3 ч. рИс. 2.15. Сходимость функции Кг(0

к стационарному значению

Пример 2.17. Найти вероятность восстановления элемента за время tB =

100 ч, если случайное время восстановления распределено нормально с мате­матическим ожиданием 7^2 = 50 ч и средним квадратическим отклонением о3 = 50 ч.

В соответствии с (2.135) имеем Рв (tB) — Ф0[(Ю0—50)/50] »= Ф0(1) = «е 0,8413.

Заметим, что в примерах 2.15 и 2.17 выбраны значения математических ожиданий и средних квадратических отклонений времени восстановления эле­мента одинаковыми, так как для экспоненциального закона Т3 = 1/ix = 1 /0,02 = 50 ч и сг2 = l/p = I /0,02 = 50 ч.

Различие в вероятностях восстановления (0,8647 и 0,8413) вызваны тем, что ис­пользованы разные распределения.

Пример 2.18. В условиях примера 2.17 найти значение /в, при котором восстановление элемента произойдет с вероятностью 0,99.

Используя табл. П.4 квантилей нормального распределения или табл. П. З, найдем Ф0(ыа ) = Ф0(2,326) = 0,9900, т. е. (tB — 50)/50 = 2,326, откуда

/в = 2,326 ■ 50 + 50 = 166,3 ч.

Различия в результатах примеров 2.16 и 2.18(230,3 и 166,3 ч) вызваны тем, что экспоненциальное распределение имеет менее крутую правую ветвь плотности вероятности.

Пример 2.19. В условиях примера 2.13 найти математическое ожидание числа отказов элемента за пять лет работы.

Так как время работы t = 5 лет = 5 • 365 • 24 = 43 800 ч достаточно вели­ки по сравнению с временем жизни Тг= 5000 ч, используем асимптотическое рас­пределение числа отказов с математическим ожиданием (2.129):

tl(Tt + Т2) = 43800/(5000 + 50) да 7,96.

Пример 2.20. В условиях примера 2.19 найти вероятность того, что за пять лет работы число отказов будет не более 9, если дисперсия времени жизни и вос — t іановления of = 5002 ч2 и of = 502 ч2»

За / = 43 800 ч по (2.129) найдем дисперсию числа отказов:

( сті + al) *КТї + гг)3 = (5002 + 50а) 43 800/(5000 + 500)3 = 0,0665.

Искомая вероятность определяется табличной функцией (см. табл. П. З)

Р{г < 9) =Ф0 [(9 — 7,9б)/]/0,0665 j =Ф0 (4,033) =0,99997.

Пример 2.21. В условиях примера 2.20 найти вероятность того, что сум­марная наработка S восстанавливаемого элемента за пять лет будет не менее 39 300 ч.

В соответствии с (2.136) найдем математическое ожидание и дисперсию асим­птотического нормального распределения случайной величины S:

TifKTi-Ь Т2) = 5000 — 43800/(5000 + 500) = 39818,6 ч;

Г1Г1(0?/Г1 + аУТ2) 1 _ 5000а ■ 5002 (500+5000“ + 50а/500*) 43 800 (Тг + Т2)3 " (5000 + 5б0)3

= 32907,6 ч2.

Искомая вероятность определяется табличной функцией (табл. П. З) и с уче­том (2.97) может быть вычислена следующим образом:

. PB (S > 39300) = 1 — PU(S < 39300) = 1 — Ф0 [(39 300— 39818,6)/р/~32907,6] =
= Ф0 [(39818,6 — 39300)/181,4] = Ф0 (2,859) = 0,99788.